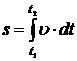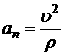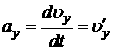Механика. Лекции по физике
- Механика. Лекции по физике
- КИНЕМАТИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.
- ДИНАМИКА. ЗАКОНЫ НЬЮТОНА
- СИЛЫ В МЕХАНИКЕ
- ИМПУЛЬС ТЕЛА. ИМПУЛЬС СИЛЫ. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА.
- ЦЕНТР МАСС. ЗАКОН ДВИЖЕНИЯ ЦЕНТРА МАСС.
- ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.
- РАБОТА И ЭНЕРГИЯ.
- ОСНОВНЫЕ ЗАКОНЫ АЭРО- И ГИДРОМЕХАНИКИ.
- ОСНОВЫ РЕЛЯТИВИСТСКОЙ МЕХАНИКИ.
- Примеры решения задач
- Тема «Законы Ньютона»
- Тема «Импульс тела. Центр масс»
- Тема «Динамика вращательного движения»
- Тема «Работа. Механическая энергия»
- Тема «Уравнения гидродинамики»
МЕХАНИКА.
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА.
Перемещением материальной точки за время ![]() называется вектор
называется вектор ![]() , соединяющий начальное и конечное положение этой точки. Путь
, соединяющий начальное и конечное положение этой точки. Путь ![]() — расстояние, пройденное точкой по траектории за время
— расстояние, пройденное точкой по траектории за время ![]() (рис.1).
(рис.1).
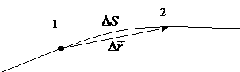 |
Рис.1.
Средней скоростью движения за время ![]() называется величина
называется величина
Скорость точки (ее также называют мгновенной скоростью)
![]() - перемещение за малое время
- перемещение за малое время ![]() . Вектор
. Вектор ![]() направлен по касательной к траектории движения, т.к. при
направлен по касательной к траектории движения, т.к. при ![]() вектор
вектор ![]() , секущий траекторию, становится касательным к ней вектором
, секущий траекторию, становится касательным к ней вектором ![]() .
.
Т.к. модуль перемещения ![]() и расстояние
и расстояние ![]() , пройденное за малое время, совпадают, то модуль вектора скорости равен производной от пути
, пройденное за малое время, совпадают, то модуль вектора скорости равен производной от пути ![]() по времени
по времени ![]()
Соответственно путь ![]() , пройденный за время
, пройденный за время ![]() , равен интегралу от скорости
, равен интегралу от скорости ![]() по времени
по времени ![]()
Движение материальной точки также описывают с помощью ее координат ![]() . В этом случае, чтобы определить скорость
. В этом случае, чтобы определить скорость ![]() , сначала вычисляют проекции скорости на оси x,y,z , которые равны производным от соответствующих координат по времени
, сначала вычисляют проекции скорости на оси x,y,z , которые равны производным от соответствующих координат по времени
Тогда величина скорости
Ускорение характеризует быстроту изменения скорости
![]() — изменение вектора скорости за малый промежуток времени
— изменение вектора скорости за малый промежуток времени ![]() .
.
Ускорение ![]() можно разложить на тангенциальное (его еще называют касательным) ускорение
можно разложить на тангенциальное (его еще называют касательным) ускорение ![]() и нормальное (центростремительное) ускорение
и нормальное (центростремительное) ускорение ![]() ,
,
Тангенциальное ускорение ![]() возникает, если скорость меняет величину, оно равно производной от скорости
возникает, если скорость меняет величину, оно равно производной от скорости ![]() по времени
по времени ![]() ,
,
При движении с постоянной по величине скоростью ![]() .
.
Нормальное ускорение
![]() - радиус кривизны траектории в данной ее точке. Радиус кривизны
- радиус кривизны траектории в данной ее точке. Радиус кривизны ![]() равен радиусу окружности, дуга которой совпадает с участком траектории.
равен радиусу окружности, дуга которой совпадает с участком траектории.
Для траектории, представляющей собой прямую линию, ![]() и
и 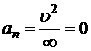 . Т.е. нормальное ускорение возникает только при искривлении траектории движения, когда вектор скорости
. Т.е. нормальное ускорение возникает только при искривлении траектории движения, когда вектор скорости ![]() меняет свое направление.
меняет свое направление.
Если траектория точки — окружность, то радиус кривизны равен радиусу окружности, ![]() , и
, и 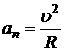 .
.
Тангенциальное ускорение ![]() направлено по касательной к траектории; направление
направлено по касательной к траектории; направление ![]() совпадает с направлением вектора скорости
совпадает с направлением вектора скорости ![]() при ускоренном движении и противоположно ему при замедленном. Нормальное ускорение
при ускоренном движении и противоположно ему при замедленном. Нормальное ускорение ![]() перпендикулярно
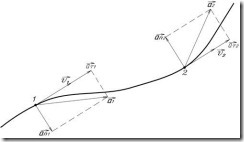
перпендикулярно ![]() и направлено в сторону вогнутости траектории (рис.2). Т.к. векторы
и направлено в сторону вогнутости траектории (рис.2). Т.к. векторы ![]() и
и ![]() перпендикулярны, то величина полного ускорения
перпендикулярны, то величина полного ускорения
Рис.2.
При координатном способе задания движения, чтобы определить ускорение, сначала вычисляют его проекции на оси x,y,z
Величина ускорения в этом случае
3. Формулы прямолинейного равноускоренного движения.
Если тело (материальная точка) движется вдоль оси х с постоянным ускорением, проекция которого на эту ось равна ![]() , то зависимость координаты тела
, то зависимость координаты тела ![]() от времени
от времени ![]() описывается уравнением
описывается уравнением
Проекция ![]() скорости в момент
скорости в момент ![]() равна
равна
![]() — начальная координата и
— начальная координата и ![]() — проекция скорости на ось х в момент времени
— проекция скорости на ось х в момент времени ![]() .
.
Формулы равноускоренного движения используются при решении задач на падение тел вблизи поверхности Земли, т.к. такое движение происходит под действием силы тяжести с постоянным ускорением ![]() м/c2 (ускорение свободного падения тел).
м/c2 (ускорение свободного падения тел).
4. Поступательное движение тела.
Поступательным называется движение, при котором любая прямая, проведенная в теле, перемещается параллельно самой себе. Т.к. при поступательном движении траектории, скорости и ускорения всех точек тела совпадают, то для описания движения тела достаточно рассмотреть движение любой его точки.
- Prev
- Вперёд >>